What on Earth is integration
 |
Contents |
Imagine you have a graph. And on it you’ve got some sort of curve or line or whatever. And lets say that just for the fun of it you wanted to find the area between the curve and the x-axis of the graph. If you have a straight line its relatively easy, you’ll either have a rectangular area a triangular area or a combination of the two. But what if you have a curve, and it’s a real evil looking curve at that? Well you use integration.
Now unless you know the exact equation of the curve or line or whatever, you can’t use integration. Hell, if you don’t know the exact equation of the line I can’t think of much you can do.
I’ve Got My Equation, What Next?
First you need to pick an axis to integrate to. Do you want to find the area under the curve (x-axis) or next to the curve (y-axis). Next you need to pick you limits. Where does your area go between? 5 and 7? -21 and 2.4? 0 and ∞? Once you have your limits and your axis of choice you can set it all out nice and neat in integral form so it looks something like this
(1) ![]()
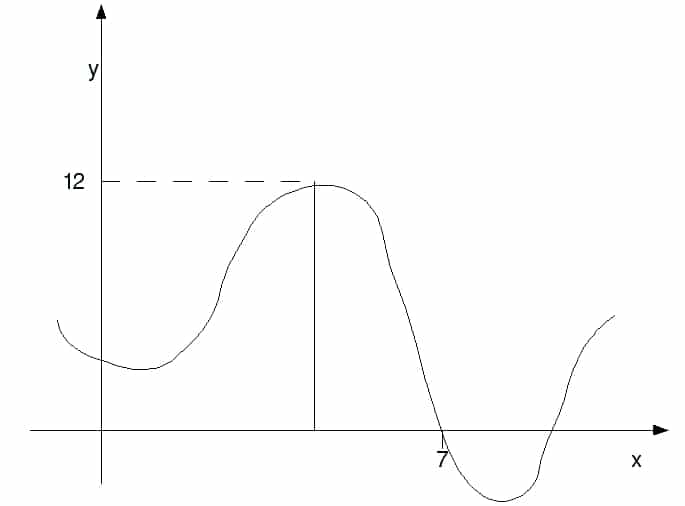
a and b are your limits, how big your area is, which numbers it’s going between. Now say you’ve decided to integrate some horrible equation to find its area. And you’ve decided to work to the x-axis between 0 and 7, like so

What integrating does is basically split it into loads of little bits and add them up e.g. one of the little bits of the graph would be this
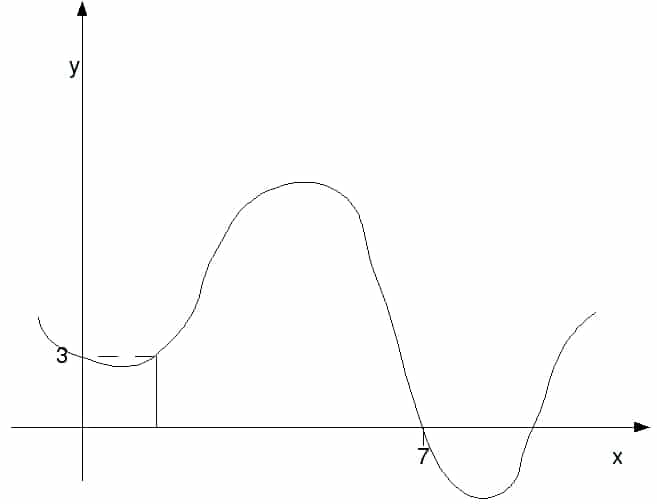 and all others in between your two limits (in this case 0 and 7). Integrating does this for you. It takes into account an infinite number of strips all with 0 width and allows you to work out the total area. So let’s go back to the integral (equation 1)
and all others in between your two limits (in this case 0 and 7). Integrating does this for you. It takes into account an infinite number of strips all with 0 width and allows you to work out the total area. So let’s go back to the integral (equation 1)
(2) ![]()
The curly bit in front of the integral is just like a stretched s and it basically stands for “sum” because what you’re doing is adding up all the little bits. The .dx bit in the integral is just there to show you that you are adding up all the bits along the x-axis. d”something” in maths nearly always means “a small change in something”.
So between the big s with your limits and the .dx bit at the end you have your f(x). Now you may not be familiar with this notation so I’ll explain. f(x) this is just some function of x. f(x) just means this is where you put your function of x, be it sin(x), x2+23, or whatever, just something where it’s the x that’s changing. If you had y=x3+3x+4 then your f(x) is just x3+3x+4, that’s your function.
Doing the Integral
Since I’ve already typed it in and can just use copy and paste lets integrate y=x3+3x+4 between 5 and 9. This could go horribly wrong but I’m now determined to stick with it.
So first let’s write it out in its proper form like so
(3) ![]()
Now the integrating part…
It was at this point I realised I was stuck. There is no set of rules for all of Integration, you have to do different things depending on what kind of equation you have. Some equations integrate nicely, some dont, for some you have to use multiple rules. What I’ll do is start off basic and work up to the hard stuff.
Simple Powers
Ok, back to the equation we had before, y=x3+3x+4 between 5 and 9. So you put it in the standard form for integrals and get
(4) ![]()
Now to integrate. To integrate all you do is a certain operation on all of the terms that need it. In this case we have the .dx at the end so its the x‘s were interested in, so we have to perform this special operation on all of the terms that feature an x. Now the first and possibly the most fundamental and basic rule of integration is
(5) ![]()
Any time you have an x to a simple numerical power you just follow the rule here. Just add 1 to the power and then divide the whole thing by the new power, so x2 becomes x3/3 and x57.8 becomes x58.8/58.8. If the term doesnt contain an x term, say for example 8, then you just say that it’s 8x0 since x0 is 1, so when you integrate 8 you get 8x. So with the example
(6) ![]()
This however is just a standard integral, its like a formula for the area, so to actually find the area we have to do it like this
(7) ![]()
To finally solve the bit on the right in the square brackets with the limits you just put the top limit in for x and then take away from that the value for when the bottom limit is x, like so
(8) ![]()
So the area under the graph of y=x3+3x+4 between 5 and 9 is just 1584
Fractions
For a fraction where the only denominator is x to a power you can use a method that allows you to treat it like we did in the Simple Powers section. The method is to use the following relationship
Tricky Functions
If you have looked through this page and been unable to find a rule for your function, that may be because there isn’t one. Some equations don’t have nice rules and sometimes they need multiple ones. There is a fantastic resource on wikipedia that may help you with some of the more complicated equations, you can find it HERE! (Of course we hope you found the answer here)